Hình chóp có các cạnh bên bằng nhau là một dạng hình chóp đặc biệt, tuy nhiên, nó chưa đủ điều kiện để được gọi là hình chóp đều. Để hiểu rõ hơn, chúng ta cùng tìm hiểu về hình chóp đều và các dạng hình chóp cụ thể như hình chóp tam giác đều và hình chóp tứ giác đều.
Hình chóp đều được định nghĩa là hình chóp có đáy là một đa giác đều và hình chiếu của đỉnh chóp xuống đáy trùng với tâm của đa giác đều đó. Điều này đồng nghĩa với việc tất cả các cạnh bên của hình chóp đều có độ dài bằng nhau.
Một tính chất quan trọng của hình chóp đều là chân đường cao của nó chính là tâm của đáy. Công thức tính thể tích hình chóp đều được cho bởi: V = (1/3) S h, trong đó S là diện tích đáy và h là chiều cao của hình chóp.
Hình chóp tam giác đều là một trường hợp cụ thể của hình chóp đều, với đáy là một tam giác đều. Các mặt bên của hình chóp tam giác đều là các tam giác cân bằng nhau. Chân đường cao của hình chóp tam giác đều trùng với trọng tâm của tam giác đáy.
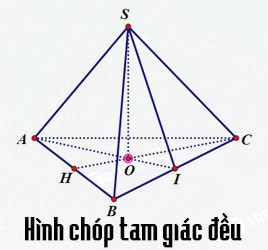 Hình chóp tam giác đều với các cạnh bên bằng nhau
Hình chóp tam giác đều với các cạnh bên bằng nhau
Hình chóp tứ giác đều cũng là một dạng hình chóp đều, nhưng đáy của nó là một hình vuông. Tương tự như hình chóp tam giác đều, các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau, và chân đường cao trùng với tâm của hình vuông đáy (giao điểm của hai đường chéo).
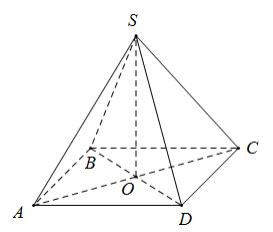 Hình chóp tứ giác đều với đáy hình vuông và các cạnh bên bằng nhau
Hình chóp tứ giác đều với đáy hình vuông và các cạnh bên bằng nhau
Vậy, một hình chóp có các cạnh bên bằng nhau chưa chắc đã là hình chóp đều. Nó chỉ là hình chóp đều khi đáy của nó là một đa giác đều và hình chiếu của đỉnh xuống đáy trùng với tâm của đa giác đều đó. Nếu đáy không phải là đa giác đều, thì hình chóp đó chỉ đơn giản là hình chóp có các cạnh bên bằng nhau.
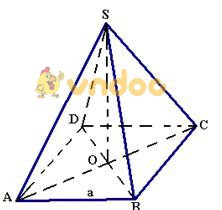 Hình minh họa hình chóp tứ giác đều và công thức tính thể tích
Hình minh họa hình chóp tứ giác đều và công thức tính thể tích
Phân biệt hình chóp tam giác đều và hình chóp tứ giác đều khá đơn giản: hình chóp tam giác đều có đáy là tam giác đều, còn hình chóp tứ giác đều có đáy là hình vuông. Mặc dù cả hai đều có các cạnh bên bằng nhau, nhưng hình dạng đáy khác nhau dẫn đến các tính chất và công thức tính toán khác nhau.









Ý kiến bạn đọc (0)