Cái gì của ta chặt không đứt dứt không ra là cái gì?

Bài toán lớp 4 từng gây khó khăn cho nhiều người lớn với câu hỏi “cái gì của ta chặt không đứt, dứt không ra” thực chất là một bài toán hình học thú vị. Câu đố này ám chỉ mối quan hệ giữa diện tích mảnh vườn và cái lều hình vuông bên trong. Dưới đây là phân tích chi tiết bài toán và cách giải:

Bài toán gốc:

Một cái lều hình vuông nằm giữa mảnh vườn hình vuông. Khoảng cách từ mỗi cạnh lều đến tường rào vườn là 8m. Tổng diện tích phần vườn không tính lều là 448 m2. Tính diện tích cái lều.

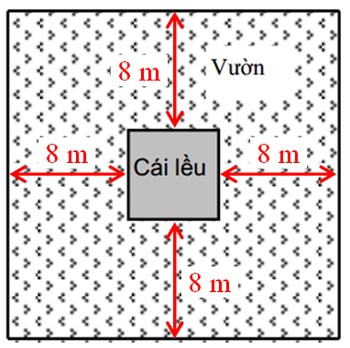Bài toán gốc

Bài toán nâng cao:

Một cái lều hình vuông nằm trong mảnh vườn hình vuông. Hiệu độ dài cạnh vườn và cạnh lều là 16m. Tổng diện tích phần vườn không tính lều là 448 m2. Tính diện tích cái lều trong các trường hợp:

a. Cạnh lều song song với cạnh vườn. (Có thể cho khoảng cách từ lều đến tường rào là (4m, 12m) hoặc (3m, 13m) để bài toán dễ hơn).

b. Cạnh lều không song song với cạnh vườn.

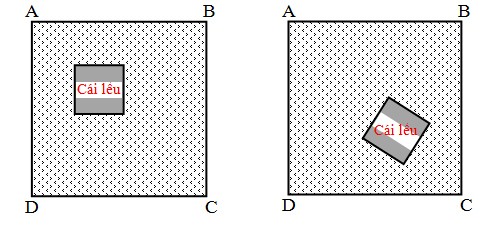Minh họa bài toán nâng cao

Lời giải (cho cả hai trường hợp):

Diện tích phần vườn không bị lều che phủ không đổi dù vị trí lều thay đổi. Ta có thể di chuyển lều đến vị trí thuận tiện để tính toán.

Cách 1:

Di chuyển lều vào giữa vườn. Vì hiệu cạnh vườn và cạnh lều là 16m, khoảng cách từ mỗi cạnh lều đến tường rào là 8m (giống bài toán gốc).

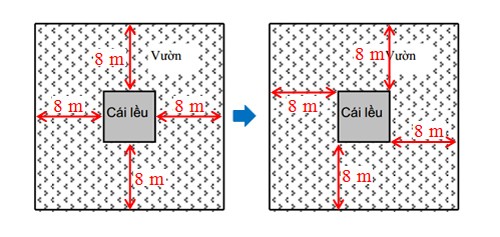Minh họa cách giải 1

Chia vườn thành 4 hình chữ nhật bằng nhau, tổng diện tích 448 m2. Diện tích mỗi hình chữ nhật là 112 m2. Chiều rộng hình chữ nhật là 8m, nên chiều dài là 112 : 8 = 14m. Chiều dài hình chữ nhật bằng cạnh lều cộng 8m, vậy cạnh lều dài 6m. Diện tích lều là 6 x 6 = 36 m2.

Cách 2:

Di chuyển lều vào một góc vườn.

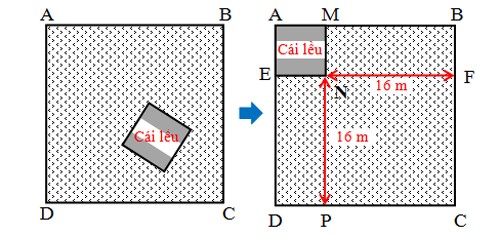Minh họa cách giải 2

Hiệu cạnh vườn và cạnh lều là 16m, nên NF = NP = 16m, MN = EN.

Diện tích vườn = Diện tích CPNF + Diện tích MBFN + Diện tích DPNE = 16 x 16 + 16 x MN + 16 x EN = 256 + 32 x MN.

Diện tích vườn là 448 m2, nên 256 + 32 x MN = 448. Vậy MN = 6m.

Diện tích lều là 6 x 6 = 36 m2.